Skip to main content

Uniswap: How to calculate Impermanent Loss?

Impermanent Loss is a popular concept when it comes to automated market makers and decentralized exchanges like Uniswap. This term is often defined as the percentage loss a liquidity provider would experience for a given price movement. This means that, as an LP, your position may fall in value due to volatility, causing a loss compared to holding these assets outside of the pool. 

This article will spell out the concept in mathematical logic and explain all the assumptions involved. 

We consider a market with liquidity L and amounts x and y of assets X and Y respectively. We also have P as the price of X in terms of Y, and a price movement P1 = P.d where d >0

According to the definition of IL touched upon, we establish a generic formula for IL:

where:
  • V1 is the value of your position in the pool at the price P1 (x,y move with price)
  • Vh is the value of your assets at the price P1 if you keep them outside of the pool 
  • We also consider V0 as the initial value of your holding (at the price P)

Impermanent Loss on Uniswap V2

On Uniswap V2, we have constant product formula and the price between X and Y:


It follows then that:



When the price move to P1, we have V1 in terms of L and P1:

and also have Vh in terms of L and P1:


By combining (3) and (4), we can easily derive the formula for IL:


Impermanent Loss on Uniswap V3

On the Uniswap V3, reserves for a concentrated position are described by the curve:


We will use the same approach to calculate IL for V3 based on the above V2 section, and also define Pa, Pb to be the price interval for our concentrated position. Both P and P1 are assumed to be inside this range. 

On the other hand, we can also determine the amounts x and y in terms of real and virtual reserves. And note that the amounts of reserves of your position are now x_r and y_r:

Now, we combine (1), (2) with the V3 curve, then the real reserves are described like this:


The initial value V0 of your holding:


When the price move to P1, the real reserves x_r and y_r also change and V1 is just V0 with P1 substituted for P:

Next up is Vh:

Finally, we calculate IL on V3 as a percentage change:

We also can described IL(V3) in terms of IL(V2): 


Note that we don't use this equation if the price falls outside the liquidity range [Pa, Pb].


Labels

Labels:

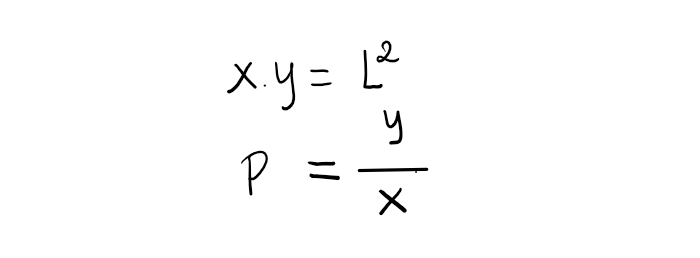
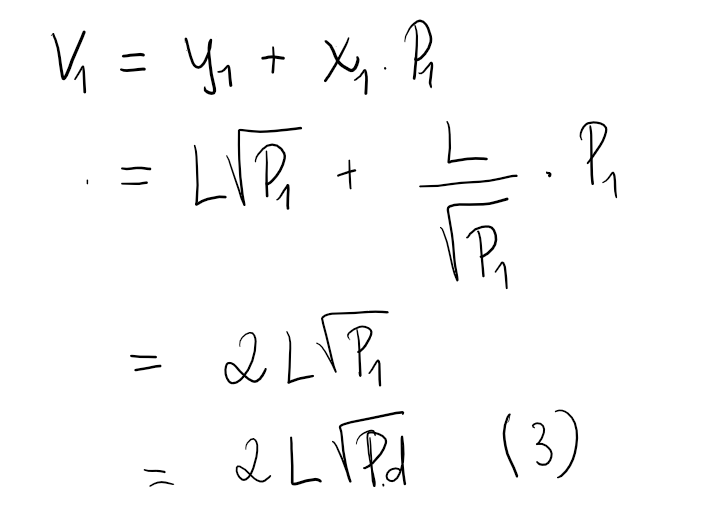
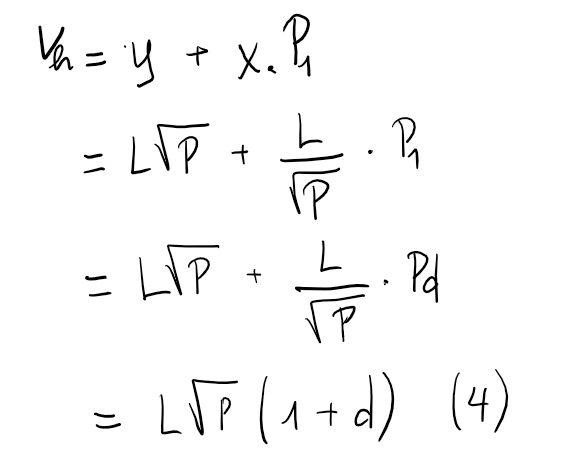
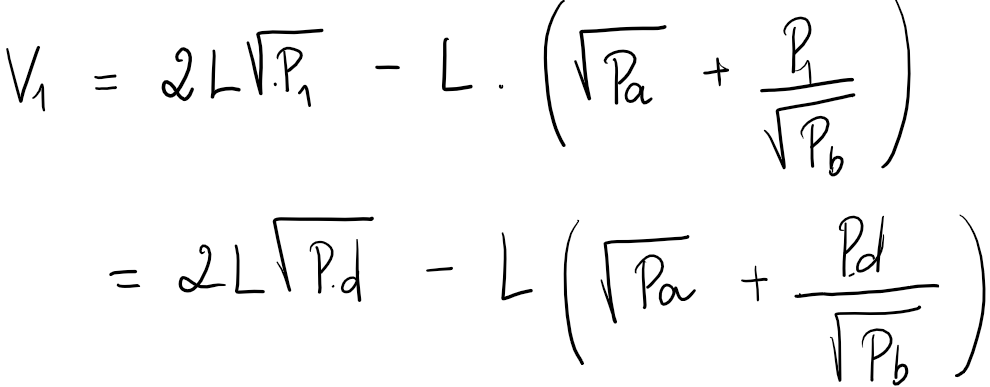
Comments

Post a Comment

Popular posts from this blog

DeFi Summary Q3 2022

DeFi protocols have begun to shift in their business life cycle, with some dApps even showing periods of profitability  Regulatory Actions Q3 has been an active period for regulators. The US SEC claimed that it has jurisdiction over Ethereum transactions because nodes are clustered more densely in the US than in any other country. According to Ehernode's data, roughly 45% of Ethereum validator nodes operate from the US, with Germany in a distant second at 12% and Singapore at 4%. Below it shows the estimated geographic distribution of Ethereum nodes worldwide.  In August, the US Treasury sanctioned the cryptocurrency mixer, Tornado Cash. This is seemingly the first time the Treasury sanctioned a piece of code (as opposed to an individual or entity) but likely not the last. The CFTC has also been active, issuing a settlement order finding that Ooki DAO and its founders violated the Commodity Exchange Act and applying a $250k fine. The Commission defines the Ooki DAO unincorpora...
Post a Comment
Read more

The FTX Collapse

This situation is a mess. Some of the information here might be outdated by the time you read this, and we might have missed today's breaking news, but this is our attempt to give you some sort of overview of the situation. So: FTX reportedly used customers' funds to prop up Alameda Research and has now filed for Chapter 11 bankruptcy.  Yes, one of the largest crypto companies in the industry was playing with customers' money An embarrassment for the industry, but it also reminds us of what an unregulated wild west this still is. The beloved CEO of FTX, Sam Bankman-Fried, a self-proclaimed supporter of effective altruism, a friend of politicians in Washington, and the world's richest 30-year-old just a week ago, went from hero to zero. We still don't know all the details, but the most plausible explanation for the collapse of FTX is the connection to its own trading desk, Alameda Research. FTX reportedly covered up losses for Alameda with customer funds, which resul...
Post a Comment
Read more